Sponsor
National Science Foundation, CMMI –14355262017
Bansal, Manish; Kianfar, Kiavash
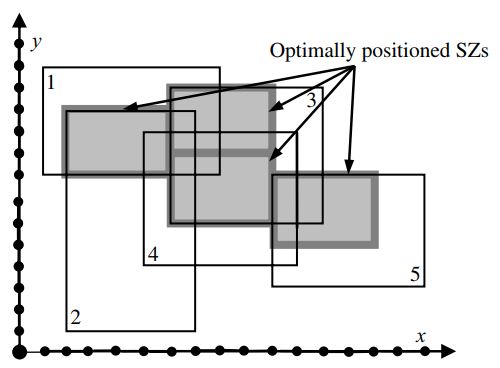
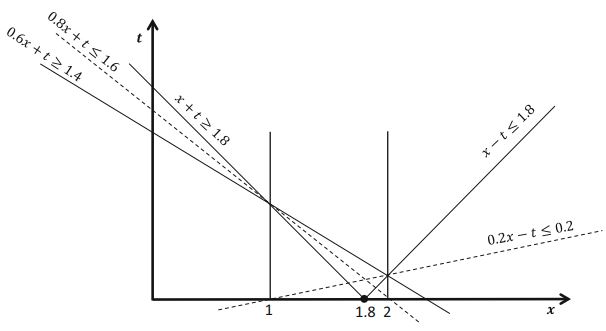
Planar Maximum Coverage Location Problem with Partial Coverage and Rectangular Demand and Service Zones Journal Article
In: INFORMS Journal on Computing, vol. 29, pp. 152-169, 2017.
@article{Bansal2017b,
title = {Planar Maximum Coverage Location Problem with Partial Coverage and Rectangular Demand and Service Zones},
author = {Manish Bansal and Kiavash Kianfar},
url = {https://doi.org/10.1287/ijoc.2016.0722},
year = {2017},
date = {2017-01-03},
journal = {INFORMS Journal on Computing},
volume = {29},
pages = {152-169},
abstract = {We study the planar maximum coverage location problem (MCLP) with rectilinear distance and rectangular demand zones in the case where “partial coverage” is allowed in its true sense, i.e., when covering part of a demand zone is allowed and the coverage accrued as a result of this is proportional to the demand of the covered part only. We pose the problem in a slightly more general form by allowing service zones to be rectangular instead of squares, thereby addressing applications in camera view-frame selection as well. More specifically, our problem, referred to as PMCLP-PCR (planar MCLP with partial coverage and rectangular demand and service zones), is to position a given number of rectangular service zones (SZs) on the two-dimensional plane to (partially) cover a set of existing (possibly overlapping) rectangular demand zones (DZs) such that the total covered demand is maximized. Previous studies on (planar) MCLP have assumed binary coverage, even when nonpoint objects such as lines or polygons have been used to represent demand. Under the binary coverage assumption, the problem can be readily formulated and solved as a binary linear program; whereas, partial coverage, although much more realistic, cannot be efficiently handled by binary linear programming, making PMCLP-PCR much more challenging to solve. In this paper, we first prove that PMCLP-PCR is NP-hard if the number of SZs is part of the input. We then present an improved algorithm for the single-SZ PMCLP-PCR, which is at least two times faster than the existing exact plateau vertex traversal algorithm. Next, we study multi-SZ PMCLP-PCR for the first time and prove theoretical properties that significantly reduce the search space for solving this problem, and we present a customized branch-and-bound exact algorithm to solve it. Our computational experiments show that this algorithm can solve relatively large instances of multi-SZ PMCLP-PCR in a short time. We also propose a fast polynomial time heuristic algorithm. Having optimal solutions from our exact algorithm, we benchmark the quality of solutions obtained from our heuristic algorithm. Our results show that for all the random instances solved to optimality by our exact algorithm, our heuristic algorithm finds a solution in a fraction of a second, where its objective value is at least 91% of the optimal objective in 90% of the instances (and at least 69% of the optimal objective in all the instances).},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2016
Sanjeevi, Sujeevraja; Masihabadi, Sina; Kianfar, Kiavash
Using cuts for mixed integer knapsack sets to generate cuts for mixed integer polyhedral conic sets Journal Article
In: Mathematical Programming, vol. 159, pp. 571-583, 2016, ISSN: 0025-5610.
@article{Sanjeevi2016,
title = {Using cuts for mixed integer knapsack sets to generate cuts for mixed integer polyhedral conic sets},
author = {Sujeevraja Sanjeevi and Sina Masihabadi and Kiavash Kianfar},
url = {https://doi.org/10.1007/s10107-015-0959-1},
issn = {0025-5610},
year = {2016},
date = {2016-09-01},
journal = {Mathematical Programming},
volume = {159},
pages = {571-583},
abstract = {Based on a bijective mapping between two mixed integer sets, we introduce a new perspective on developing cuts for the mixed integer polyhedral conic (MIPC) set by establishing a one-to-one correspondence between the cuts for this set and those for a related mixed integer knapsack (MIK) set. The face/facet-defining properties of the corresponding cuts are identical for their respective sets. We further show that the cut generation approach for the MIPC set resulting from this new perspective always produces cuts that dominate those generated based on any of the two individual MIK constraints corresponding to the MIPC constraint. Our computational results show this dominance can be quite significant. As a special case of this new perspective, the conic MIR inequality of Atamtürk and Narayanan for the MIPC set and its properties can be directly derived from the MIR inequality for the MIK set and its properties. We also generalize these cuts to the n-step conic MIR inequalities, which are directly derived form the n-step MIR inequalities for the MIK set.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2015
Bansal, Manish; Kianfar, Kiavash
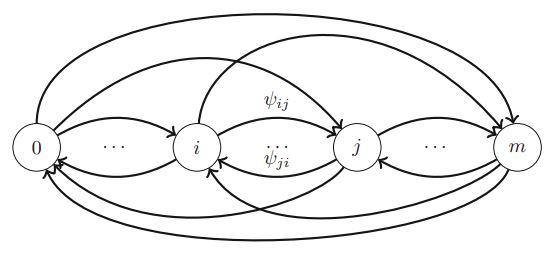
n-Step cycle inequalities: facets for continuous multi-mixing set and strong cuts for multi-module capacitated lot-sizing problem Journal Article
In: Mathematical Programming, vol. 154, pp. 113-144, 2015, ISSN: 0025-5610.
@article{Bansal2015,
title = {n-Step cycle inequalities: facets for continuous multi-mixing set and strong cuts for multi-module capacitated lot-sizing problem},
author = {Manish Bansal and Kiavash Kianfar},
doi = {https://doi.org/10.1007/s10107-015-0906-1},
issn = {0025-5610},
year = {2015},
date = {2015-04-28},
journal = {Mathematical Programming},
volume = {154},
pages = {113-144},
abstract = {In this paper, we introduce a generalization of the continuous mixing set, which we refer to as the continuous multi-mixing set. This set is closely related to the feasible set of the multi-module capacitated lot-sizing (MML) problem with(out) backlogging. We present a family of valid inequalities for the continuous multi-mixing set and identify conditions under which they are facet-defining. The cycle inequalities, n-step MIR inequalities, and mixed n-step MIR inequalities are special cases of these inequalities. We also present an exact separation algorithm for our inequalities. We then use these inequalities to generate valid inequalities for MML with(out) backlogging. Our computational results show that our cuts are very effective in solving the MML instances, resulting in substantial reduction in the integrality gap, number of nodes, and total solution time.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Cost-Effective Capacity Planning Involving Differently Sized Capacity Modules
Cost-effective operation of many systems critical to the U.S. economy and society, such as power grids, data centers, telecommunication networks, medical facilities, on/off-shore pipelines, transportation, construction, production, and service systems, is highly dependent on cost-effective planning of capacity installation/deployment/usage in these systems (e.g., for processing, transmission, transportation, production, or service capacity). The concept of capacity in these systems is oftentimes modular, i.e., the total capacity is composed of identical capacity modules that are installed/deployed/used as needed. Cost-effective capacity planning in such systems is a challenging problem. Mixed integer programming is well suited to model this problem but to date research on mixed integer programming cutting plane theory has almost entirely focused on problems with a single modularity (module size). This is while in the aforementioned systems, the available capacity modules are, almost always, of several different sizes, which makes cost-effective capacity planning much more challenging.
This research aims to address this gap by developing and evaluating cutting planes to solve mixed integer programs involving multi-modularity capacity constraints with a particular focus on multi-modularity capacitated lot-sizing, facility location, and network design. The complex integer rounding methodologies developed by the investigation team in their previous project provide an appropriate machinery to initiate this research.
Complex Integer Rounding Cuts for Mixed Integer Programming
The overarching goal of this research is to create and evaluate new cutting plane methods for mixed integer programming using a new approach here called Complex Integer Rounding. It involves the generalization of Mixed Integer Rounding (MIR) in several fundamental ways. The general approach is to identify and study the structure of simple polyhedra and use them to develop new general cuts. Both single-constraint and multi-constraint cuts are considered and facet-defining properties of the developed cuts are investigated. The customization of the cuts to a collection of important special-structure problems is studied. In order to evaluate performance of the developed cuts, efficient separation methods are developed and comprehensive computational experiments are performed.
Sponsor
National Science Foundation, CMMI –11003432015
Bansal, Manish; Kianfar, Kiavash
n-Step cycle inequalities: facets for continuous multi-mixing set and strong cuts for multi-module capacitated lot-sizing problem Journal Article
In: Mathematical Programming, vol. 154, pp. 113-144, 2015, ISSN: 0025-5610.
@article{Bansal2015,
title = {n-Step cycle inequalities: facets for continuous multi-mixing set and strong cuts for multi-module capacitated lot-sizing problem},
author = {Manish Bansal and Kiavash Kianfar},
doi = {https://doi.org/10.1007/s10107-015-0906-1},
issn = {0025-5610},
year = {2015},
date = {2015-04-28},
journal = {Mathematical Programming},
volume = {154},
pages = {113-144},
abstract = {In this paper, we introduce a generalization of the continuous mixing set, which we refer to as the continuous multi-mixing set. This set is closely related to the feasible set of the multi-module capacitated lot-sizing (MML) problem with(out) backlogging. We present a family of valid inequalities for the continuous multi-mixing set and identify conditions under which they are facet-defining. The cycle inequalities, n-step MIR inequalities, and mixed n-step MIR inequalities are special cases of these inequalities. We also present an exact separation algorithm for our inequalities. We then use these inequalities to generate valid inequalities for MML with(out) backlogging. Our computational results show that our cuts are very effective in solving the MML instances, resulting in substantial reduction in the integrality gap, number of nodes, and total solution time.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
2012
Sanjeevi, Sujeevraja; Kianfar, Kiavash
Mixed n-step MIR inequalities: Facets for the n-mixing set Journal Article
In: Discrete Optimization, vol. 9, pp. 216-235, 2012.
@article{Sanjeevi2012,
title = {Mixed n-step MIR inequalities: Facets for the n-mixing set},
author = {Sujeevraja Sanjeevi and Kiavash Kianfar},
url = {https://doi.org/10.1016/j.disopt.2012.07.003},
year = {2012},
date = {2012-11-01},
journal = {Discrete Optimization},
volume = {9},
pages = {216-235},
abstract = {Günlük and Pochet [O. Günlük, Y. Pochet, Mixing mixed integer inequalities. Mathematical Programming 90 (2001) 429–457] proposed a procedure to mix mixed integer rounding (MIR) inequalities. The mixed MIR inequalities define the convex hull of the mixing set and can also be used to generate valid inequalities for general as well as several special mixed integer programs (MIPs). In another direction, Kianfar and Fathi [K. Kianfar, Y. Fathi, Generalized mixed integer rounding inequalities: facets for infinite group polyhedra. Mathematical Programming 120 (2009) 313–346] introduced the n-step MIR inequalities for the mixed integer knapsack set through a generalization of MIR. In this paper, we generalize the mixing procedure to the n-step MIR inequalities and introduce the mixed n-step MIR inequalities. We prove that these inequalities define facets for a generalization of the mixing set with integer variables in each row (which we refer to as the n-mixing set) . The mixed MIR inequalities are simply the special case of . We also show that mixed n-step MIR can generate valid inequalities based on multiple constraints for general MIPs. Moreover, we introduce generalizations of the capacitated lot-sizing and facility location problems, which we refer to as the multi-module problems, and show that mixed n-step MIR can be used to generate valid inequalities for these generalizations. Our computational results on small MIPLIB instances as well as a set of multi-module lot-sizing instances justify the effectiveness of the mixed n-step MIR inequalities.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
Kianfar, Kiavash
On n-step MIR and partition inequalities for integer knapsack and single-node capacitated flow sets Journal Article
In: Discrete Applied Mathematics, vol. 160, pp. 1567-1582, 2012.
@article{Kianfar2012,
title = {On n-step MIR and partition inequalities for integer knapsack and single-node capacitated flow sets},
author = {Kiavash Kianfar},
url = {https://doi.org/10.1016/j.dam.2012.02.025},
year = {2012},
date = {2012-07-01},
journal = {Discrete Applied Mathematics},
volume = {160},
pages = {1567-1582},
abstract = {Pochet and Wolsey [Y. Pochet, L.A. Wolsey, Integer knapsack and flow covers with divisible coefficients: polyhedra, optimization and separation, Discrete Applied Mathematics 59 (1995) 57–74] introduced partition inequalities for three substructures arising in various mixed integer programs, namely the integer knapsack set with nonnegative divisible/arbitrary coefficients and two forms of single-node capacitated flow set with divisible coefficients. They developed the partition inequalities by proving properties of the optimal solution in optimizing a linear function over these sets. More recently, the author and Fathi [K. Kianfar, Y. Fathi, Generalized mixed integer rounding inequalities: facets for infinite group polyhedra, Mathematical Programming 120 (2009) 313–346] have introduced the n-step mixed integer rounding (MIR) inequalities for the mixed-integer knapsack set with arbitrary coefficients through a generalization of MIR. In this paper, we show that the n-step MIR generates facet-defining inequalities not only for the three sets considered by Pochet and Wolsey but also for their generalization to the case where coefficients are not necessarily divisible. In the case of divisible coefficients, n-step MIR directly generates the partition inequalities for all three sets (and in some cases stronger inequalities for one of the sets). We show that n-step MIR gives facets for the integer knapsack set with arbitrary coefficients that either dominate or are not obtainable by the partition inequalities. Also, using the n-step MIR, we introduce families of facets for the two capacitated flow sets with arbitrary coefficients for the first time. Our results provide a new perspective based on n-step MIR into the polyhedral properties of these three substructures, extend them to the case of arbitrary coefficients, and underscore the power of n-step MIR to easily generate strong valid inequalities.},
keywords = {},
pubstate = {published},
tppubtype = {article}
}
